Jeux de semailles et information

Qu’est-ce que l’aléatoire ? Pour répondre à cette question, la théorie de la complexité de Kolmogorov répond que plus un objet (ou un algorithme) paraît complexe, plus il est aléatoire. Et Kolmogorov mesure la complexité d’un objet (une structure de données par exemple) par la longueur d’un algorithme permettant de construire cet objet. Cette idée, trop abstraite pour figurer un jour au programme d’informatique, s’illustre bien dans l’étude de jeux de semailles malawites.

En 1913, Meredith Sanderson, médecin colonel de l’armée britannique au Malawi (alors Nyasaland), publie dans le journal de l’institut royal anthropologique, un article titré Native Games of Central Africa, où il décrit des jeux de semailles au nom imprononçable, qui se jouent sur des plateaux de 4 rangées (2 rangées par joueur), comme ceci :

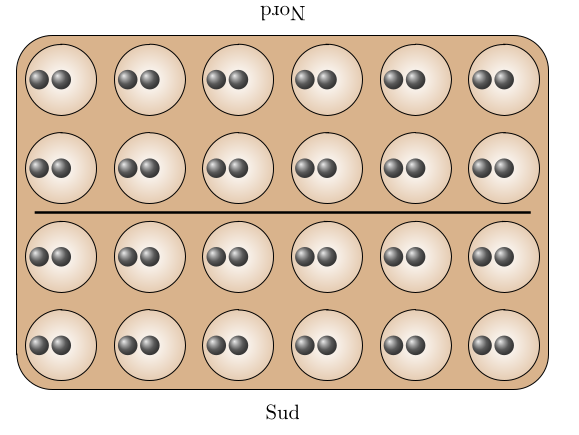
Le plateau ci-dessus est celui du nchuwa avant de jouer. Le jeu se déroule en trois phases :

1. une phase préliminaire qui fait l’objet de cet article et qu’on détaillera donc plus bas,
2. le jeu normal (règle ci-après) tant qu’au moins une case contient plusieurs graines (et alors on doit jouer une de ces cases),
3. lorsque toutes las cases non vides sont des singletons (ne contiennent qu’une graine chacune), on a le droit de jouer une de ces cases singleton, mais uniquement si la case d’arrivée est vide, et prioritairement si cela permet de capturer des graines à l’adversaire.

Chaque joueur à son tour sème les graines d’une case (contenant au moins 2 graines) dans le sens trigonométrique (comme dans les jeux de l’hémisphère Nord), représenté par des flèches (bleues pour Sud, rouges pour Nord) sur ce graphique :

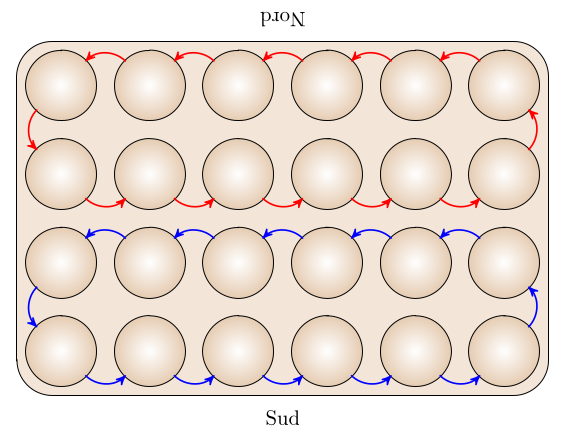
Si la dernière graine du semis tombe dans une case non vide (qui contient donc au moins 2 graines) on prend toutes ces graines et on les resème (comme dans les jeux asiatiques). Le tour de jeu ne s’achève que lorsque la dernière graine tombe dans une case vide (comme dans les jeux asiatiques mais aussi un jeu dahoméen du XIX^e siècle). Au moment où le tour de jeu s’arrête, si la dernière graine est tombée dans une case vide de la rangée intérieure, alors

• s’il y a des graines juste en face (dans la rangée intérieure de l’adversaire), on les capture (elles sont alors définitivement retirées du plateau),
• si, en plus, il y a aussi des graines dans la même colonne mais au fond (rangée extérieure de l’adversaire), on les capture aussi.

(dans le cas particulier du nchuwa, on peut aussi capturer les graines d’une autre case de l’adversaire, ce qui accélère le jeu par rapport aux variantes qu’on verra plus bas)

Le but du jeu est de prendre toutes les graines de l’adversaire.

Mais en fait, aucun des jeux observés par Sanderson n’a une configuration initiale aussi simple que 2 graines par case. Sanderson décrit des algorithmes pour (re)constituer la position initiale. On va les détailler ci-dessous.

Nchuwa

La configuration initiale est en fait celle-ci :

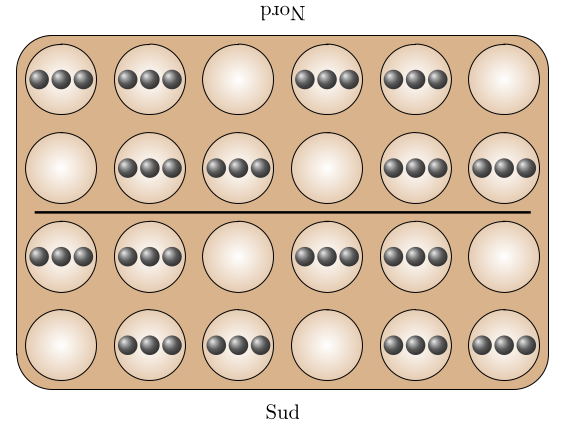
Pour obtenir cette position, on part de celle où il y a 2 graines par case, puis

• on sème vers la gauche (sans resemer) celles qui sont à droite dans la rangée intérieure,
• on sème les deux graines de la case suivante (troisième case en partant de la gauche), toujours vers la gauche,
• on sème les deux suivantes (première case de la rangée extérieure) mais vers la droite (en fait on suit le circuit),
• et on sème les deux graines qui sont dans la quatrième case à partir de la gauche (toujours vers la droite).

L’algorithme peut se résumer à : on sème dans le sens trigonométrique à partir de la case à droite de la rangée intérieure, la première case qu’on trouve et qui contient deux graines, jusqu’à ce qu’il ne reste que des cases à trois graines.

Cet algorithme, ainsi que la position de départ (2 graines par case) est plus facile à retenir que la vraie position initiale (3 graines par case mais où sont les cases vides ?). Ceci illustre la théorie de Kolmogorov : au lieu de mémoriser l’information qui se trouve dans le plateau de jeu, il est plus facile de mémoriser l’algorithme, ce qui revient à compresser l’information. D’ailleurs l’entropie du plateau avec 2 graines par case est 4,584962500721156 alors que celle de la vraie position initiale est 4 qui est plus petite.

Njombwa

avec 61 graines

Dans le jeu de njombwa, la position initiale est celle-ci :

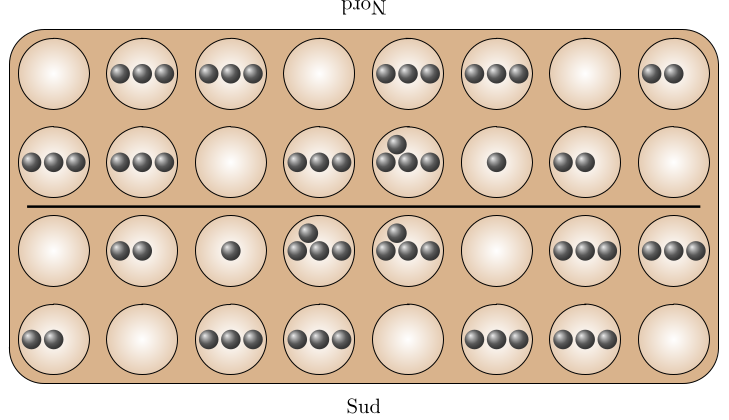
L’entropie de ce plateau est 4,392810492839524 qui est voisine de celle du jeu nchuwa, mais Sanderson donne un algorithme permettant de construire ce plateau à partir de celui ci-dessous, d’entropie beaucoup pus faible puisqu’environ égale à 1,5349547231656377 :

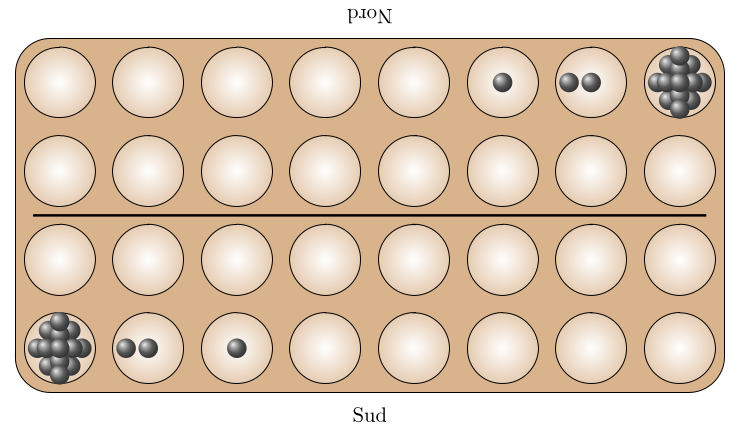
Chaque case d’angle contient 29 graines.

Voici l’algorithme :

• Nord sème les deux graines vers sa droite,
• Sud fait pareil,
• chacun son tour sème les deux graines dans le sens trigonométrique,
• mais lorsque la seconde graine tombe en face d’une case occupée, on capture la (ou les) graine(s) de cette case (ce qui fait qu’au début du jeu, il n’y a que 61 graines) et on passe à l’étape suivante (dès la première capture),
• puis Nord (et ensuite Sud) sème les 29 graines, répétitivement, jusqu’à ce que la dernière graine tombe dans une case vide.

En résumé, on met ses 32 graines dans les cases en bas à gauche, dans l’ordre (29,2,1), puis chacun son tour sème 2 graines, jusqu’à la première capture, et ensuite on sème ses 29 graines jusqu’à ce que la dernière graine tombe dans une case vide. Cet algorithme est plus facile à retenir que la répartition avant de jouer.

Dans ce jeu, on ne capture que les graines de la colonne où est tombée la dernière graine (si celle-ci est tombée dans la rangée intérieure), ce qui fait que le jeu est plus simple que le nchuwa. Il faut dire que ce jeu est celui des Yao, proches du Mozambique (et par-delà, de Madagascar), alors que le nchuwa était joué par les Tonga, plus proches de la Zambie (et par-delà, de l’ex Zaïre) où plusieurs jeux comprennent la capture dans plus de deux cases.

avec 28 graines

Dans cette variante du njombwa, le plateau initial (juste avant de jouer) est celui-ci, d’entropie 3,8073549220576055 :

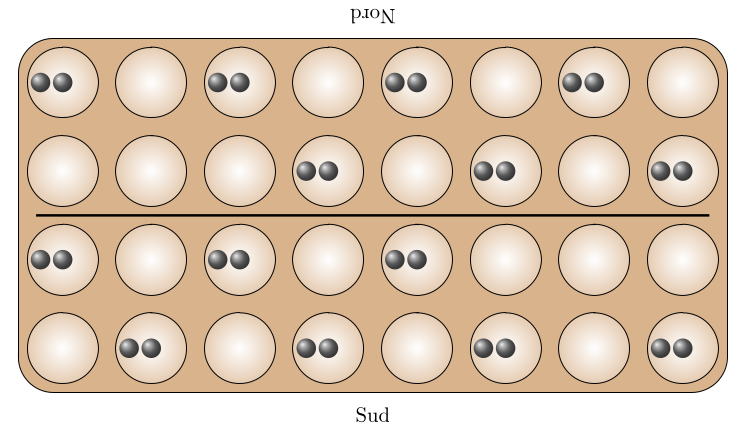
Sanderson donne un algorithme pour créer ce plateau à partir de celui-ci, d’entropie 5 :

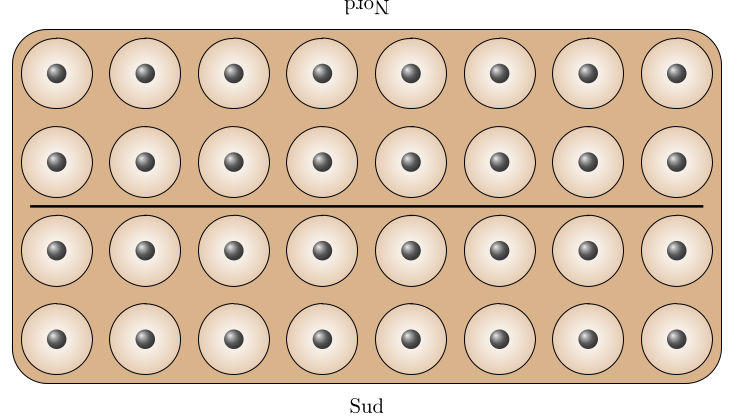
Voici l’algorithme :

• semer la graine qui est dans la case en bas à droite, dans le sens trigonométrique, et répétitivement, jusqu’à ce qu’on ait fait un tour,
• transférer dans la case en bas à droite, les deux graines qui sont là où est tombée la dernière graine,
• retirer du plateau les deux graines de droite dans la rangée intérieure.

avec 58 graines

Pas besoin d’algorithme pour trouver la position initiale, d’entropie 4,8924637537482605 :

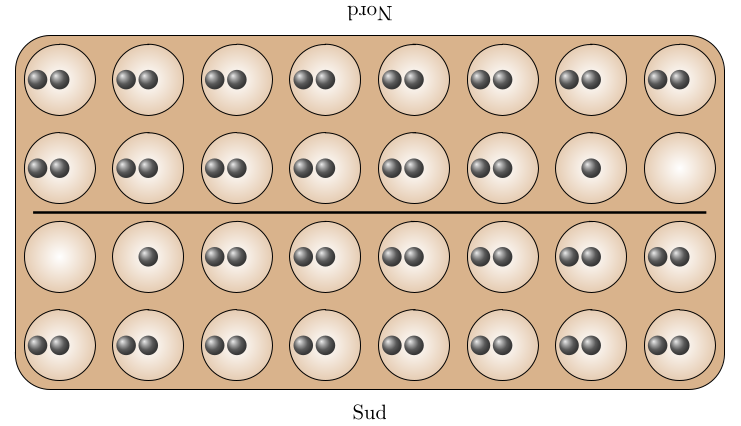
Mais on peut quand même : mettre 2 graines dans chaque case, puis vider la dernière case (en haut à gauche) et enlever une graine de l’avant-dernière case.

Msuwa na kunja

Dans ce jeu, la disposition initiale (d’entropie 4) est simple :

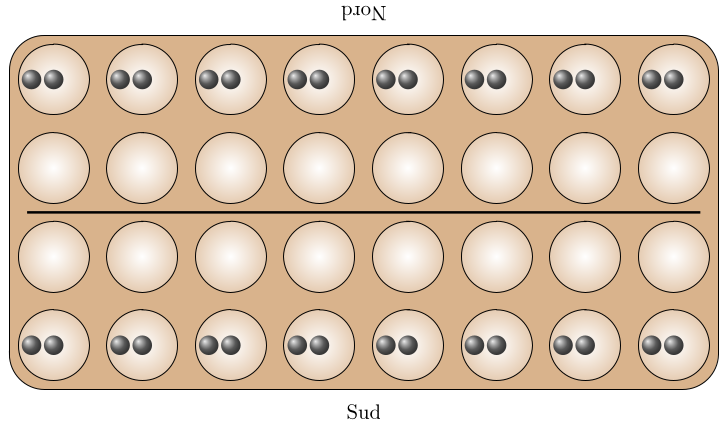
Mais on peut aussi la recréer par un algorithme : placer une graine par case, puis transférer les graines (par colonne) de la rangée intérieure vers la rangée extérieure. L’algorithme fait baisser d’une unité l’entropie du plateau.

Une autre différence avec ce jeu, est que lorsqu’on a capturé les graines d’une colonne, on peut choisir 2 autres cases (et non 1 comme au njombwa) dont on capture les graines. Cela tend à accélérer le jeu.

Spreta

Dans ce jeu, la position initiale (d’entropie 4,875) est celle-ci:

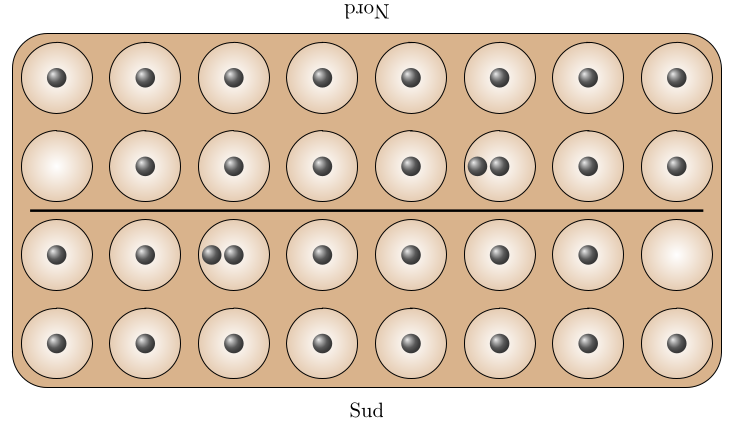
On peut la reconstituer à partir du plateau à une graine par case, en transférant la graine qui est en haut à droite, dans la troisième case à partir de la gauche.

Le premier tour du jeu est donc imposé puisque comme il y a une case contenant 2 graines, on ne peut jouer que cette case. Comme au msuwa na kunja, on capture depuis deux cases supplémentaires de son choix.