Réseaux de Petri

Dans un réseau de Petri, il y a des places (où on place des jetons) et des transitions (par lesquelles les jetons transitent). Par exemple, avec ce réseau de Petri (en haut de page) :

on voir deux transitions (l’une en haut, l’autre en bas) et chacune des deux ne peut se déclencher que s’il y a au moins un jeton en amont. En partant de

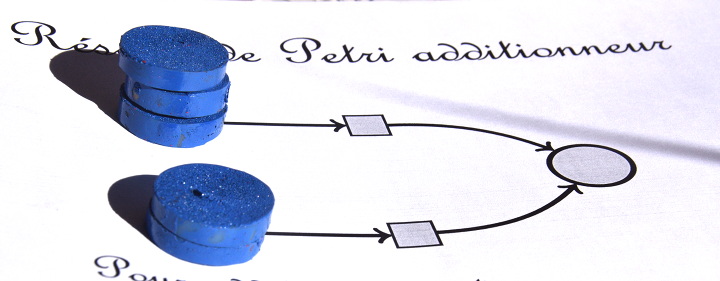
on fait évoluer le réseau de Petri tant qu’on peut, et lorsqu’aucune des deux transitions ne peut plus être déclenchée, on a :

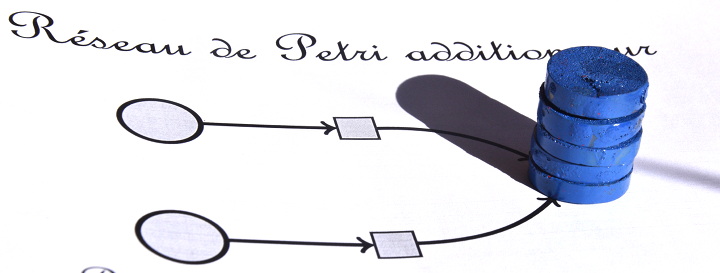
On constate que le réseau de Petri achève son calcul avec 5 jetons dans la place de droite, alors qu’il y avait en tout 5 jetons dans les places de gauche : il s’agit d’un réseau de Petri additionneur.

En fait, un réseau de Petri mène en quelque sorte un calcul. Pour trouver lequel, on peut faire tourner jusqu’à son arrêt (lorsqu’aucune transition n’est déclenchable) le réseau de Petri, et noter les états initial et final comme ceci (pour le réseau de Petri ci-dessus) :

haut	bas	droite
3	2	5
2	3	5
5	3	8
0	2	2

Ce réseau de Petri (celui du haut) calcule simultanément la différence et le minimum de deux nombres entiers :

Par exemple, avec 5 et 2 :

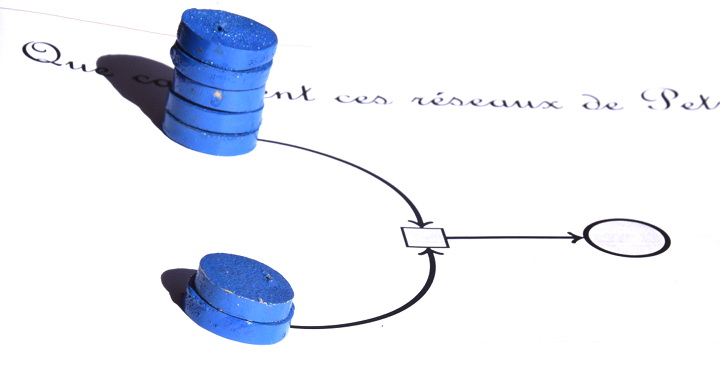
il calcule 5-2 (à gauche) et le minimum de 5 et 2 (à droite) :

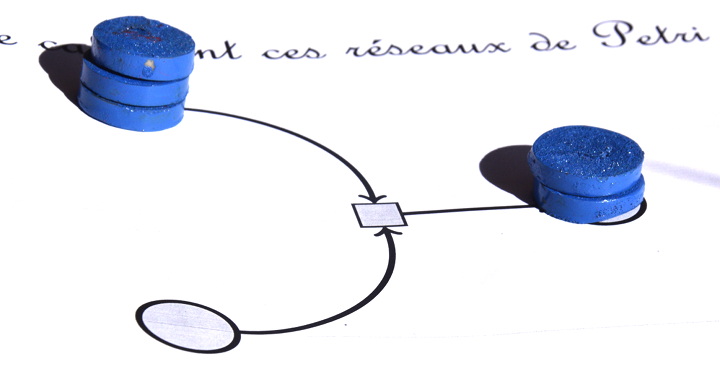
En fait, un réseau de Petri peut calculer toute fonction sous-linéaire (inférieure ou égale à une fonction affine) comme la racine carrée ou le logarithme.

Réseaux de Petri à arcs inhibiteurs

En ajoutant des arcs inhibiteurs (représentés par des ronds : la présence d’au moins un jeton en amont de l’arc inhibiteur empêche la transition de se déclencher, même s’il y a suffisamment de jetons en amont de celle-ci), on peut calculer tout ce qui est calculable avec un tel réseau de Petri.

Un théorème dit qu’avec 3 arcs inhibiteurs, on peut calculer toute fonction calculable avec un réseau de Petri. Avec les réseaux de Petri à un ou deux arcs inhibiteurs, on dispose donc d’une puissance de calcul qui couvre plus que les fonctions sous-linéaires et moins que les fonctions calculables. On ne sait pas quelles sont ces fonctions. En tout cas, avec deux arcs inhibiteurs on peut faire des multiplications :

Voici un exemple d’utilisation de ce réseau de Petri (pour vérifier que 3×2=6) :

Peut-on faire un réseau de Petri multiplicateur avec un seul arc inhibiteur ? En tout cas, si on va jusqu’à trois arcs inhibiteur, on peut calculer tout ce qui est calculable, comme la division euclidienne :

ou un calcul de PGCD :

Ce réseau de Petri est une représentation graphique de l’algorithme d’Euclide, à 6 arcs inhibiteurs. Voici la preuve par Petri du fait que 5 et 3 sont premiers entre eux (à la fin il ne reste qu’un jeton là où initialement il y en avait 5) :

Jeux sur réseaux de Petri

Les réseaux de Petri permettent de modéliser des jeux de Nim, comme par exemple le jeu de Fort Boyard :

ou d’autres, comme ce réseau de Petri inventé pour servir de plateau de jeu :

D’autres exemples (y compris un compteur binaire) sont présents ici :

Réseaux de Petri et écologie

Les réseaux de Petri permettent aussi de modéliser les interactions entre populations, comme ce modèle proie-prédateur discret :