Sofus (le nom est un hommage à Sophus Lie), qui a sa chaîne youtube, est à la fois
- un langage de programmation Turing-complet (inspiré de Cobol),
- une webApp permettant de programmer en Sofus
- des interpréteurs (en Python par exemple) pour calculatrices telles la Numworks…
On programme en ligne, avec des blocs similaires à ceux de Scratch, par exemple si on veut simuler la suite de Collatz, on place des blocs ainsi :
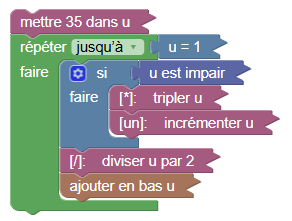
Un clic sur le drapeau vert aura alors pour effet de produire cet affichage :
53
80
40
20
10
5
8
4
2
1Sofus possède de multiples tortues (ce qui lui permet de résoudre les sujets de DNB, plutôt mieux que Scratch) et on peut utiliser la tortue pour représenter graphiquement la suite :
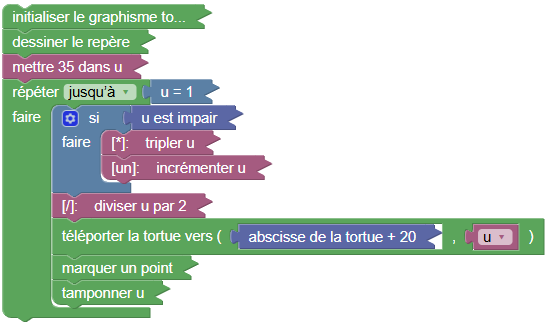
Le graphique obtenu est celui-ci :
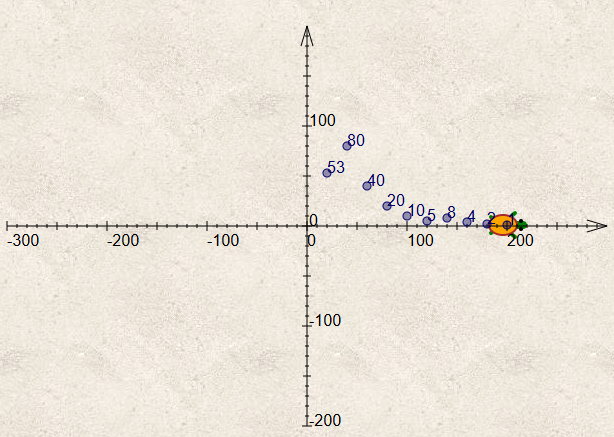
La spécialité de Sofus est surtout de pouvoir modifier une variable en place, comme le permet Python avec les +=, -=, *= et /= mais en notation préfixe (celle de Python, héritée de C, est infixe).
De Sofus vers Python avec SofusPy
Patrick Raffinat a développé une interface permettant de produire du code Python à partir des blocs de Sofus, elle s’appelle SofusPy. On peut considérer SofusPy comme un fork de Sofus, aussi un fork du fork a-t-il été produit, c’est SofusPy974.
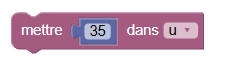
Pour programmer aisément la suite de Collatz, on peut cliquer sur le bouton commandes puis entrer
u = 35ensuite, en cliquant à nouveau sur commandes, on voit qu’un bloc est apparu :
Et, à partir de là, il est aisé de structurer le programme en insérant une boucle :
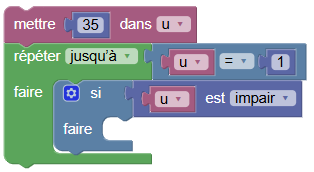
Si u est impair, on doit le tripler puis l’incrémenter. En cliquant à nouveau sur commandes, on écrit :
u*3et un nouveau clic sur commandes donne
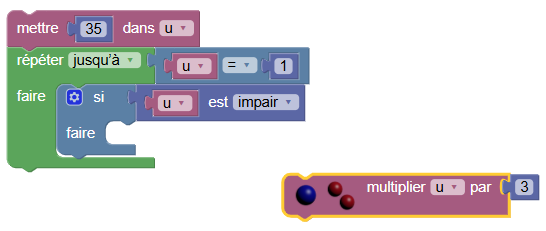
Ceci évite d’avoir à se rappeler comment on fait pour tripler une variable : SofusPy se charge de cela. Après
u+1dans les commandes, on a
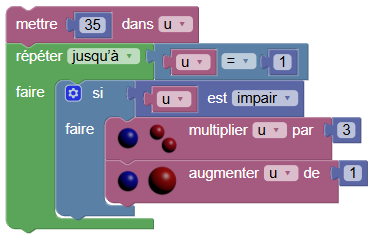
Ensuite, toujours dans les commandes, on écrit u/2 pour avoir
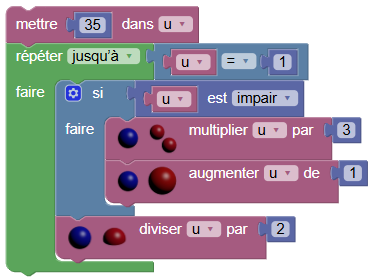
qui donne le script presque complet : il ne reste plus qu’à ajouter l’affichage (et réduire les blocs pour plus de lisibilité) :
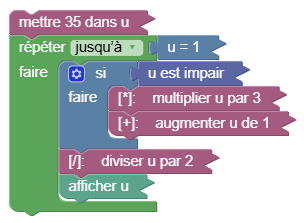
Comme dans Sofus, on peut tester le script en l’exécutant (par un clic sur le drapeau vert), mais aussi, cliquer sur le bouton Editeur qui permet de savoir comment on fait, en Python, pour tripler une variable, l’incrémenter, la diviser par 2, l’affecter, la tester, et boucler dessus :
u = 35
while not u == 1:
if u % 2 == 1:
u = u * 3
u = u + 1
u = u / 2
print(u)SofusPy974 est un accélérateur d’apprentissage de Python. Cerise sur le gâteau, il y a (dans l’éditeur Python) un bouton pseudocode qui réagit au clic en produisant, dans la fenêtre d’affichage, ce genre de prose :
u ← 35
Tant que on n'a pas u = 1
si u % 2 = 1
u ← u × 3
u ← u + 1
u ← u / 2
afficher (u)On peut bien entendu enregistrer le script Python engendré, voire utiliser la console Python pour programmer directement en ligne (sans passer par Sofus).
Sofus en cycles 3 et 4
La difficulté qu’ont des élèves de cours moyen à s’orienter dans le plan (alors même que les rotations n’y sont que d’angles droit) a mené à la création d’une autre version de Sofus, spécialisée dans le cycle 3, elle s’appelle SofusPrim.
Par ailleurs, l’abondance de programmes de calcul au DNB a mené à une intégration dans Sofus de possibilité de calcul formel permettant d’étudier des programmes de calcul. Cette nouvelle version s’appelle SofusColl. Voilà comment on peut s’en servir pour résoudre le problème de DNB Polynésie 2015 :
Voici un programme de calcul.
•Choisir un nombre
•Ajouter 1
•Calculer le carré de cette somme
•Soustraire 9 au résultat.
1.Vérifier qu’en choisissant 7 comme nombre de départ, le résultat obtenu avec ce programme est 55.
2.Lorsque le nombre choisi est −6, quel résultat obtient-on ?
4.Le programme donne 0 pour deux nombres. Déterminer ces deux nombres.
Le programme de calcul produit un résultat qui dépend du nombre choisi au départ. Conceptuellement, il s’agit d’une fonction, et le nombre qu’on lui fournit est renommé variable, car en fait 7 (dans la question 1) n’est pas un nombre, mais la valeur initiale d’une variable :
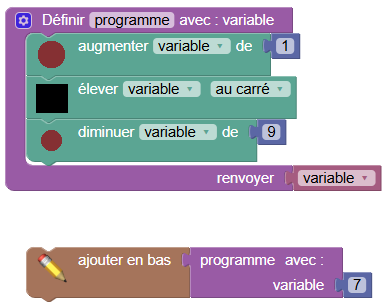
L’affichage en bas donne bien 55 (réponse à la question 1). Pour répondre à la question 2, il suffit de mettre -6 à la place de 7 :

ce qui donne dans la console :
16Pour la question 4, on gagne à nommer x le nombre choisi :

ce qui donne cet affichage :
- 8 + x**2 + 2*xOn peut faire mieux :

ce qui donne
- 8 + x² + 2 xPour résoudre la question 4, on peut faire

ce qui produit l’affichage peu lisible (mais correct) :
- 1 + (sqrt(36))/2, - 1 + (sqrt(36))/-2Mais pour peu que l’on sache que la racine carrée (sqrt) de 36 est 6, les deux solutions s’écrivent -1+6/2 et -1+6/-2 soit -1+3 et -1-3 soit encore 2 et -4. Ce qui donne envie de faire
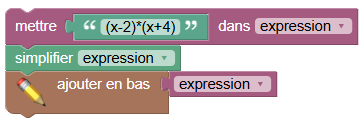
Le résultat est exactement le même que celui vu avant :
- 8 + x**2 + 2*xce qui permet de résoudre la question 4.
Remarque : la moitié environ des programmes de calcul du DNB comprennent une étape du genre soustraire le nombre de départ qui donne un graphe un peu compliqué lorsqu’on veut en représenter en flow programming (voir plus bas) et nécessite de mémoriser une copie du nombre de départ pour pouvoir exécuter ultérieurement ce genre de ligne faisant appel au nombre de départ. Cette mémorisation du nombre de départ rend d’ailleurs impossible l’usage de la mémoire de travail, et empêche de faire de ce genre de programme de calcul, un activité mentale.
Sofus, avenir des programmes de calcul ?
Sofus, créé à l’origine pour la programmation (programmes de calcul) en cycle 4, a fait ses preuves surtout en lycée (apprentissage de la programmation en maths, passage de Scratch à Python avec SofusPy974, …). Mais l’avenir des programmes de calcul (et de la programmation en général), c’est peut-être bien le flow programming, initialement popularisé dans la musique, et de plus en plus présent pour des applications plus généralistes comme Node-RED. Avec flow-974, le programme de calcul précédent se représente ainsi :
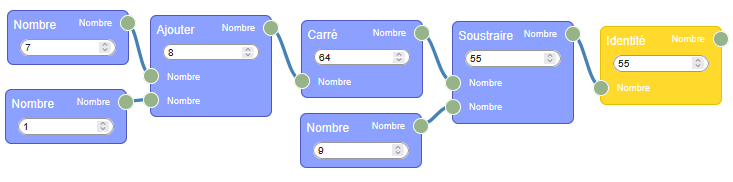
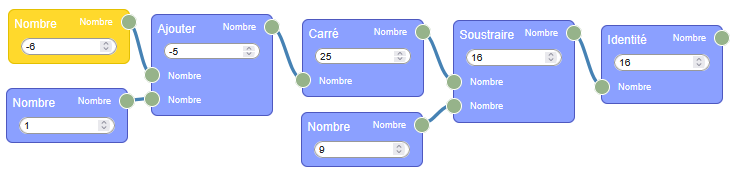
Pour la question 2, il suffit de remplacer le 7 à gauche par -6 (par exemple en cliquant 13 fois sur la flèche de décrémentation) et lire la réponse à droite :
Le flow programming permet de dessiner les combinateurs, qui sont des fonctions s’appliquant à des fonctions du même type qu’elles (voire à elles-mêmes !). Voici quelques-uns de ces dessins :
Interpréteurs Sofus
Voici un interpréteur Sofus en OCaml :
let de = "de"
let par = "par"
let dans = "dans"
let mettre d dans x = x:=d
let incrementer x = x:=!x+1
let decrementer x = x:=!x-1
let augmenter x de d = x:=!x+d
let diminuer x de d = x:=!x-d
let multiplier x par d = x:=!x*d
let diviser x par d = x:=!x/d
let doubler x = x:=!x*2
let tripler x = x:=!x*3
let quadrupler x = x:=!x*4
let quintupler x = x:=!x*5
let sextupler x = x:=!x*6
let septupler x = x:=!x*7
let octupler x = x:=!x*8
let nonupler x = x:=!x*9
let decupler x = x:=!x*10
Un autre, en Python.



Laisser un commentaire